Ejercicio resuelto TIR. SELECTIVIDAD (PAU) COMUNIDAD VALENCIANA 2018 (examen extraordinaria julio)
Ejercicio resuelto TIR. SELECTIVIDAD COMUNIDAD VALENCIANA 2018 (examen extraordinaria julio)
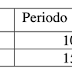
La empresa Raf S.L. desea renovar su maquinaria para cortar y pelar tomates. Se plantea dos inversiones alternativas con los siguientes flujos netos de caja esperados (en €):
Sabiendo que el coste de cada una de las máquinas es de 200 €:
a) Calcule la TIR de ambas inversiones. (Hasta 1,25 puntos)
b) Indique cuál de las dos inversiones sería más adecuada para cada una de las siguientes tasas de descuento: r1=0,08; r2=0,16; r3=0,20 (Hasta 0,75 puntos)
Solución
a) Cálculo TIR
La TIR (tasa interna de rentabilidad) nos indica cual debería ser la tasa de actualización que hace el VAN sea igual a 0. Es decir, la TIR tiene que ser mayor a la rentabilidad mínima por la que un proyecto nos sería rentable. A mayor TIR mayor rentabilidad.
Máquina 1
Si multiplicamos por (1+TIR)2 a todos los elementos de la ecuación nos queda que:
- 200 (1+TIR)2 + 100 (1+TIR) + 150
Si suponemos que (1+TIR) es igual a X
- 200 x2 + 100 x + 150
Por lo que nos queda una ecuación de segundo grado

Donde el primer elemento elevado al cuadrado es ”a” (-200) el segundo elevado a 1 es “b” (100) y el independiente es “c” (150).
El único resultado que tiene sentido en este caso es el positivo (no puede ser rentabilidad negativa para un proyecto)
Recuerda que dijimos que:
x = 1+TIR
TIR = 1,1514 - 1 = 0,1514
Si lo multiplicamos por 100 para hacerlo un porcentaje, entonces tenemos 15,14%
Lo cual quiere decir que para el proyecto la TIR = 15,14% y por tanto esa es la tasa de rentabilidad que iguala el VAN a cero. Siempre que la TIR sea mayor al valor “k” nuestro proyecto será rentable ya que en ese caso el VAN será positivo.
Máquina 2
Si multiplicamos por (1+TIR)2 a todos los elementos de la ecuación nos queda que:
- 200 (1+TIR)2 + 150 (1+TIR) +100
Si suponemos que (1+TIR) es igual a X
- 200x2 + 150 x + 100
Y por tanto
Como ya sabemos
x = 1+TIR
TIR = 1,1754 - 1 = 0,1754
Si lo multiplicamos por 100 para hacerlo un porcentaje, entonces tenemos 17,54%
Lo cual quiere decir que para el proyecto la TIR = 17,54% y por tanto esa es la tasa de rentabilidad que iguala el VAN a cero. Siempre que la TIR sea mayor al valor “k” nuestro proyecto será rentable ya que en ese caso el VAN será positivo.
b) Análisis de los resultados
Para un valor r=0,08 las dos máquinas serían rentables para la empresa ya que sus TIR son mayores.
Con un r = 0.16 la máquina 2 sería rentable (TIR = 17,54%) , pero no la 1 (TIR = 15,24%).
Con r = 0,20 ninguna de las dos opciones sería rentable para la empresa ya que ambas TIR son menores.
Y si quieres seguir repasando