Ejercicio resuelto TIR y payback. SELECTIVIDAD (PAU) COMUNIDAD VALENCIANA 2020 (examen ordinaria junio)
Ejercicio resuelto TIR y payback. SELECTIVIDAD COMUNIDAD VALENCIANA 2020 (examen ordinaria junio)
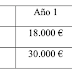
Una empresa trata de decidir entre dos proyectos de inversión cuyo desembolso inicial es el mismo e igual a 50.000 euros. Los flujos netos de caja previstos para cada proyecto se detallan en la siguiente tabla:
a) Calcule la tasa interna de rentabilidad de cada uno de los proyectos. Sabiendo que la tasa de descuento es del 6% y que la empresa sólo puede desarrollar uno de los proyectos, ¿cuál recomendaría llevar a cabo? Razone su respuesta. (Hasta 1 punto)
b) Si el objetivo de la empresa es recuperar la inversión realizada en el menor tiempo posible, ¿qué proyecto recomendaría a la empresa? Realice los cálculos necesarios para justificar su recomendación. (Hasta 1 punto)
Solución
a) Cálculo de la TIR.
La TIR (tasa interna de rentabilidad) nos indica cual debería ser la tasa de actualización que hace el VAN sea igual a 0. Es decir, la TIR tiene que ser mayor a la rentabilidad mínima por la que un proyecto nos sería rentable. A mayor TIR mayor rentabilidad.
Proyecto 1
Si multiplicamos por (1+TIR)2 a todos los elementos de la ecuación nos queda que:
- 50.000 (1+TIR)2 + 18.000 (1+TIR) + 42.000
Si suponemos que (1+TIR) es igual a X
- 50.000 x2 + 18.000 x + 42.000
Por lo que nos queda una ecuación de segundo grado

Donde el primer elemento elevado al cuadrado es ”a” (-50.000) el segundo elevado a 1 es “b” (18.000) y el independiente es “c” (42.000).
El único resultado que tiene sentido en este caso es el positivo (no puede ser rentabilidad negativa para un proyecto).
Recuerda que dijimos que:
x = 1+TIR
TIR = 1,1140- 1 = 0,1140
Si lo multiplicamos por 100 para hacerlo un porcentaje, entonces tenemos 11,40%
Lo cual quiere decir que para el proyecto la TIR = 11,40% y por tanto esa es la tasa de rentabilidad que iguala el VAN a cero. Siempre que la TIR sea mayor al valor “k” nuestro proyecto será rentable ya que en ese caso el VAN será positivo.
Proyecto 2
Si multiplicamos por (1+TIR)2 a todos los elementos de la ecuación nos queda que:
- 50.000 (1+TIR)2 + 30.000 (1+TIR) + 35.000
Si suponemos que (1+TIR) es igual a X
- 50.000 x2 + 30.000 x + 35.000
Y por tanto
Como ya sabemos
x = 1+TIR
TIR = 1,1888 - 1 = 0,1888
Si lo multiplicamos por 100 para hacerlo un porcentaje, entonces tenemos 18,88%
Lo cual quiere decir que para el proyecto la TIR = 18,88% y por tanto esa es la tasa de rentabilidad que iguala el VAN a cero. Siempre que la TIR sea mayor al valor “k” nuestro proyecto será rentable ya que en ese caso el VAN será positivo.
Análisis de los resultados
Proyecto 1
Como la TIR (11,40%) > k (6%), el proyecto es rentable.
Proyecto 2
Como la TIR (18,88%) > k (6%), el proyecto es rentable.
Ambos proyectos son rentables, pero si tuviéramos que escoger uno, nos quedaríamos con el proyecto 2, ya que tiene una TIR mayor
b) Payback
Proyecto 1
Con el Pay-Back tenemos que sumar los FNC hasta recuperar la inversión inicial (50000). Cuando lo hagamos, calcularemos el momento exacto del año en el que se produce dicha recuperación
Como el desembolso inicial son 50000 en el año 0 esa es la cantidad que falta por recuperar. Al recuperar 18000 el año 1, todavía faltan 32.000 (que ponemos con saldo negativo). Sin embargo, en el año 2 al recuperar 42.000, vemos que ya hemos recuperado todo y además sobran 10.000 (que ponemos con signo positivo).
El momento en el que recuperemos todo (los 50.000), será el plazo de recuperación. Lo normal, como vemos es que recuperemos en medio de un año y otro. Ese punto es cuando la cantidad pendiente de recuperar pasa de negativa a positiva.
Vemos que recupera su inversión inicial entre el año 1 y 2, ya que a final del año 1 quedaban por recuperar 32000, y a final del año 2 la cifra pasa a +10000 (hemos recuperado todo y nos sobra). Entre el año 1 y 2 la cifra de pendiente de recuperar pasa de negativa (-32000) a positiva (+10000).
Para saber el momento exacto que recuperamos la inversión entre el año 1 y 2, suponemos que los 42000 euros del año 2, cuando recuperamos más del desembolso inicial se reciben a lo largo del año, y queremos saber cuántos días tardará en recuperar los 32000 que le faltaban.
Por tanto, tenemos en cuenta dos puntos.
1. Cuanto dinero generé el año que recuperé el dinero y me sobró (año 242000)
2. Cuánto dinero faltaba por recuperar justo el año antes de conseguirlo (año 132000)
Genera 42000------ 12 meses
Faltan 32000-------- x meses
X = (32000*12) / 42000 = 9,14 meses
Pay back 1 = Tarda en recuperar la inversión 1 año y 9,14 meses
El proyecto es realizable ya que recupera la inversión
Proyecto 2
Vemos que recupera su inversión inicial entre el año 1 y 2, ya que a final del año 1 quedaban por recuperar 20000, y a final del año 2 la cifra pasa a +15000 (hemos recuperado todo y nos sobra). Entre el año 1 y 2 la cifra de pendiente de recuperar pasa de negativa (-20000) a positiva (+15000).
Para saber el momento exacto que recuperamos la inversión entre el año 1 y 2, suponemos que los 35.000 euros del año 2, cuando recuperamos más del desembolso inicial se reciben a lo largo del año, y queremos saber cuántos días tardará en recuperar los 20000 que le faltaban.
Por tanto, tenemos en cuenta dos puntos.
1. Cuanto dinero generé el año que recuperé el dinero y me sobró (año 235000)
2. Cuánto dinero faltaba por recuperar justo el año antes de conseguirlo (año 120000)
Genera 35000------ 12 meses
Faltan 20000-------- x meses
X = (20000*12) / 35000 = 9,14 meses
Pay back 2 = Tarda en recuperar la inversión 1 año y 6,85 meses
El proyecto es realizable ya que recupera la inversión
Entre los dos proyectos elegiremos el proyecto 2, ya que recupera antes la inversión
Y si quieres seguir repasando